Zig-Zag Numberlink (Flow Free)

A single player game in which the player connects pairs of points in a rectangular grid with paths traversing all the grid cells.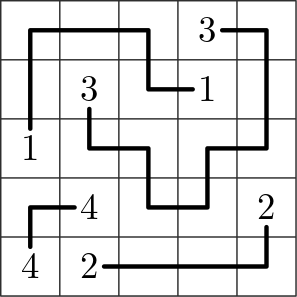

Description

Zig-Zag Numberlink is a single player game played on a rectangular grid. Initially, some of the cells of the grid are empty while others contain a number from $1$ to $k$, each of which appears exactly twice.

Each grid cells is adjacent to the cells to its left, right, top, and bottom, if any. The goal is to find a collection of $k$ simple paths (sequences of adjacent cells) such that: (i) the endpoints of the $i$-th path are the two cells containing number $i$, and (ii) each cell of the grid belongs to exactly one path.

A popular smartphone game based on Zig-Zag Numberlink is Flow Free.

Computational complexity

The problem of deciding whether an instance of Zig-Zag Numberlink admits a solution is NP-Complete [1].

Notes

The variant in which each path is required to use the minimum number of turns when considering the other paths as fixed is known as Numberlink.

References

[1] A. Adcock, E. D. Demaine, M. L. Demaine, M. P. O’Brien, F. Reidl, F. S. Villaamil, B. D. Sullivan, “Zig-Zag Numberlink is NP-Complete”, Journal of Information Processing, 2015.

▸ ▾ Cite this page

@misc{cog:zig-zag-numberlink,
    author = "{CoG contributors}",
    title  = "{Zig-Zag Numberlink (Flow Free) --- Complexity of Games}",
    year   = "2024",
    url    = "https://www.isnphard.com/i/zig-zag-numberlink/",
    note   = "[Online; accessed 2024-04-13]"
}