Numberlink

A single player game in which the player connects pairs of points in a rectangular grid with paths that traverse all the grid cells and avoid unnecessary turns.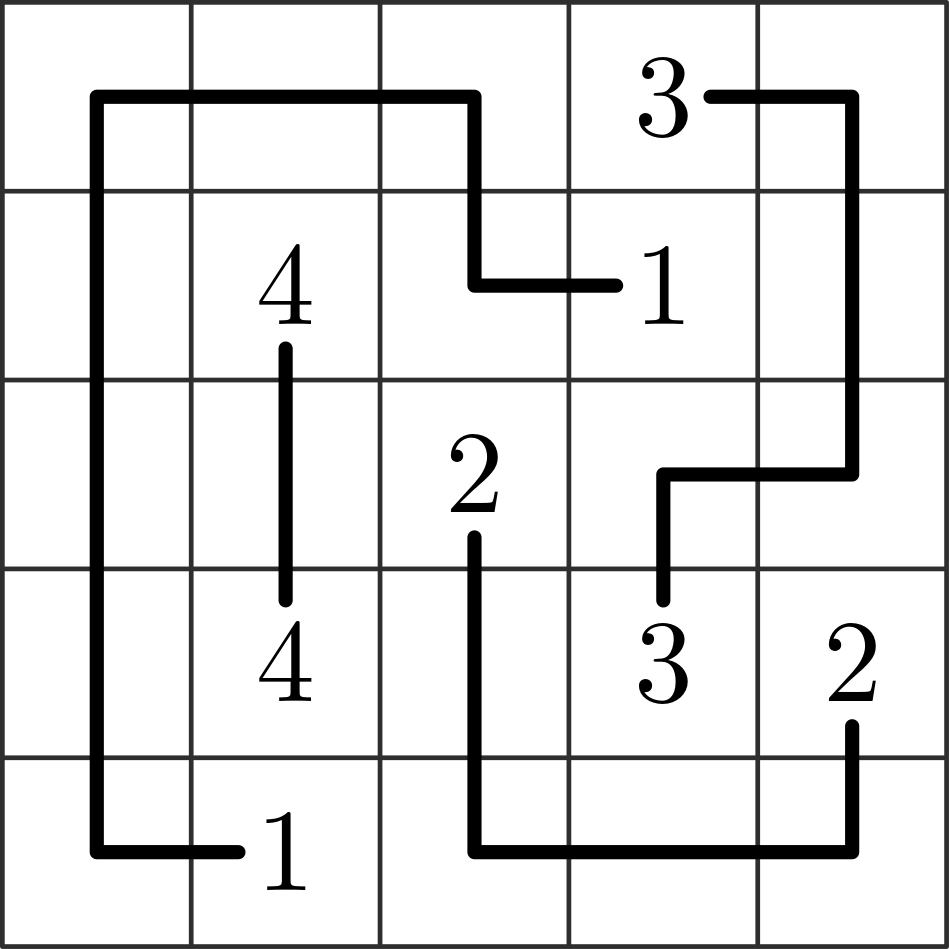

Description

Numberlink is a single player game played on a rectangular grid. Initially, some of the cells of the grid are empty while others contain a number from $1$ to $k$, each of which appears exactly twice.

Each grid cells is adjacent to the cells to its left, right, top, and bottom, if any. The goal is to find a collection of $k$ simple paths (sequences of adjacent cells) such that:

The endpoints of the $i$-th path are the two cells containing number $i$;
Each cell of the grid belongs to exactly one path; and
For each $i=1,\dots,k$ the following holds: once paths $1, \dots, i-1, i+1, k$ are fixed, the $i$-th path performs the minimum number of turns among those that satisfy the previous two conditions.

Computational complexity

The problem of deciding whether an instance of Numberlink admits a solution is NP-Complete [1].

Notes

The variant in which condition 3 is removed is known as Zig-Zag Numberlink.

References

[1] The referenced material may not have undergone a rigorous peer review process (e.g., papers on open-access repositories, personal webpages, extended abstracts, ...) K. Kotsuma, Y. Takenaga, “NP-Completeness and Enumeration of Number Link Puzzle”, IEICE Technical Report, 2010.

▸ ▾ Cite this page

@misc{cog:numberlink,
    author = "{CoG contributors}",
    title  = "{Numberlink --- Complexity of Games}",
    year   = "2024",
    url    = "https://www.isnphard.com/i/numberlink/",
    note   = "[Online; accessed 2024-05-28]"
}