Two Dots

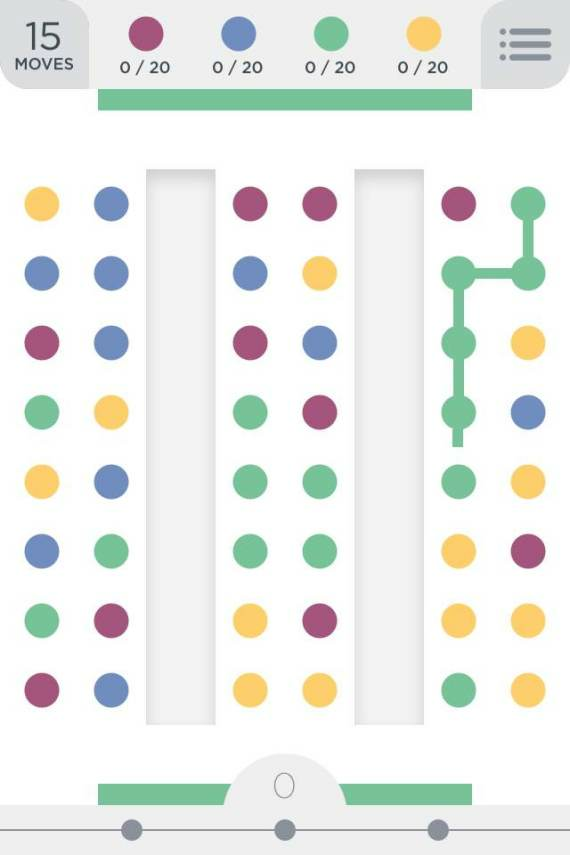
Description

A simplified version of the game is as follows: the board consists of a $n \times m$ grid in which each position is either empty or occupied by a dot having one out of $k$ colors. Dots are attracted towards the last row as if affected by gravity (i.e., in each column all the non-empty locations are contiguous and on the last rows). A move consists of either:

• Drawing a monochromatic simple path by connecting together adjacent dots. This causes all the dots of the path to be removed from the board.

• Drawing a monochromatic cycle with a (possibly empty) hanging path. This causes all the dots of cycle’s color to be removed from the board.

After each move, the remaining dots fall down to fill the now-empty locations.

There are $g$ goals $(c_1, t_1), \dots, (c_g, t_g)$ to be satisfied: each goal $(c_i, t_i)$ consists of a color $c_i$ and a positive integer $t_i$. A goal $(c_i, t_i)$ is satisfied when at least $t_i$ dots of color $c_i$ are collected.

The game is won if the player satisfies all $g$ goals within certain number $\ell$ of moves.

Computational complexity

Determining whether there exists a winning strategy is NP-Complete even in the following special cases [1]:

• $k=3$, $\ell=2$, $g=2$ via a reduction from Exact Cover by 3-Sets. An interactive version of the reduction is available here.

• $m=2, \ell=\infty$, and the only goal ($g=1$) is collecting two dots of a single color ($t_1=2)$.

• $n=2$.

The same problem is $W[ 1 ]$-hard when parameterized by $\ell$ [2], and is in P if (i) $n=1$, or (ii) $m=1$ and $g = O(1)$ [1].

References

[1] D. Bilò, L. Gualà, S. Leucci, N. Misra, “On the Complexity of Two Dots for Narrow Boards and Few Colors”, in FUN 2018.

[2] Neeldhara Misra, “Two dots is NP-complete”, in FUN 2016.

@misc{cog:two-dots,
    author = "{CoG contributors}",
    title  = "{Two Dots --- Complexity of Games}",
    year   = "2024",
    url    = "https://www.isnphard.com/i/two-dots/",
    note   = "[Online; accessed 2024-05-28]"
}