TwixT

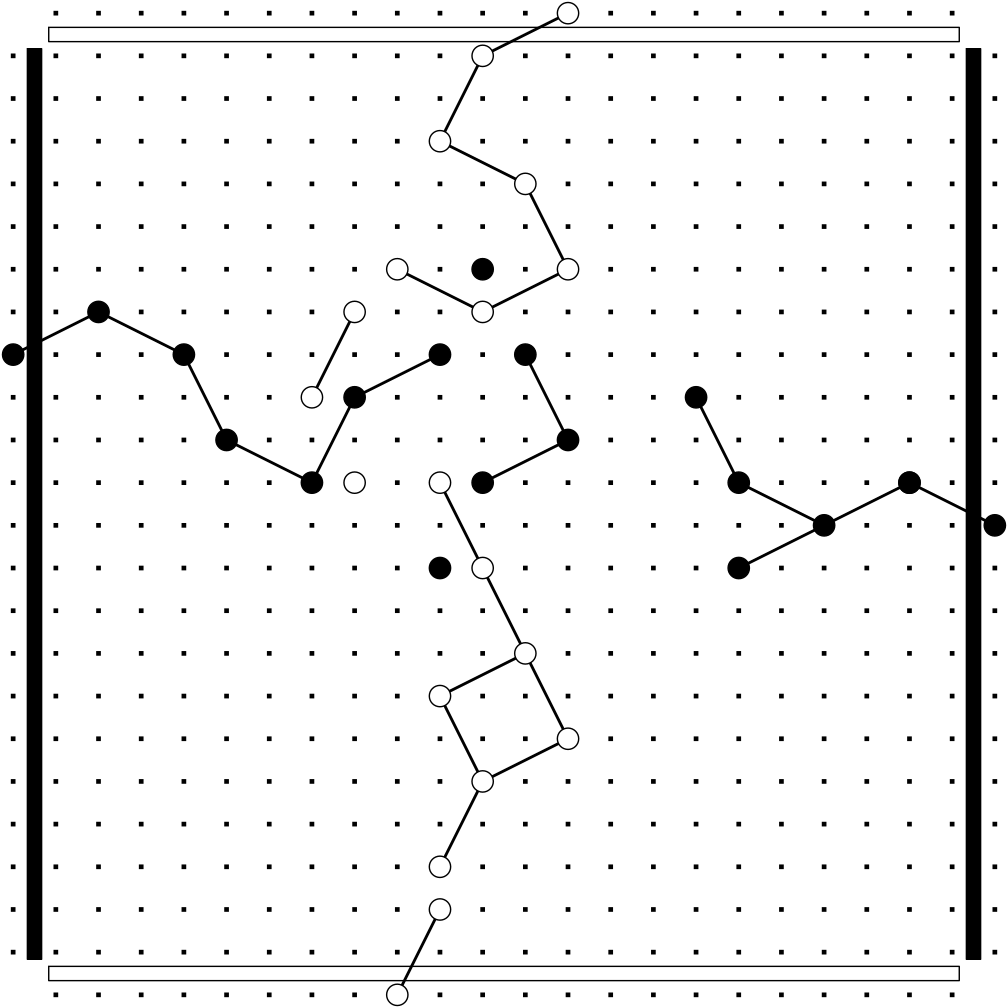
Description

The game is played by two players, Black and White, on a $n \times m$ board in which each non-corner location is a hole that can host colored pegs. The holes on two opposing sides of the board are associated with Black, and the holes on the remaining two opposing sides are associated with White. The players take turns placing a peg of their color in an empty hole that is not on one of the opponent’s sides of the board. Pegs of the same color that are a knight’s move away from each other can be linked together with a straight segment, provided that it does not cross any other segment. After placing a peg, the current player has the option to remove any number of links between pegs of their color, and to create any number of new links between pegs of their color. White moves first. Usually, after the first peg is played, Black has the option to switch sides. The game is won by the first player that manages to connect (using a chain of links) two pegs on opposite sides of the board. It is possible for the game to end in a draw.

In the classical version of the game shown, e.g., in the picture, $n = m = 24$.

Non-square boards can be used as a form of handicap (the stronger player has to connect the farthest sides).

A popular paper and pencil variant is called TwixT PP. In this variant links connecting pegs of the same color are allowed to cross, but no link can be removed.

Computational complexity

The problem of deciding whether White has a winning strategy in TwixT is PSPACE-complete [1].

References

[1] É. Bonnet, F. Jamain, A. Saffidine, “Havannah and TwixT are PSPACE-complete”, in CG 2013.

@misc{cog:twixt,
    author = "{CoG contributors}",
    title  = "{TwixT --- Complexity of Games}",
    year   = "2024",
    url    = "https://www.isnphard.com/i/twixt/",
    note   = "[Online; accessed 2024-04-13]"
}