
Trainyard
A puzzle game in which the player has to lay down tracks to get colored trains from their departure stations to a suitable destination stations.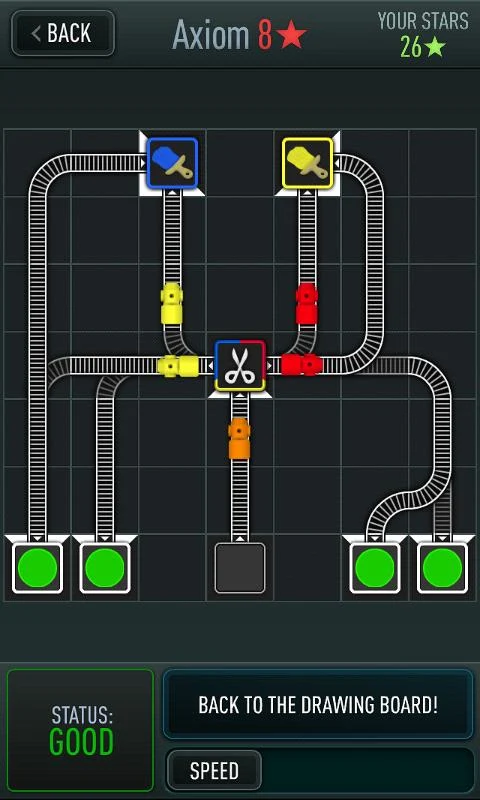
Description
The game is played in a rectangular board in which each tile is empty, blocked, a departure station, a destination station, or a special tile. Each departure station initially contains a certain number of colored trains (possibly having different colors). Each destination station accepts one or more colored trains. When two trains of different colors meet, their colors are mixed together (e.g., if a blue and yellow train meet, they both become green). Additionally, if the position and travel direction of two trains coincide, they merge into a single train.
A special tiles splits any incoming train into two trains of the constituting colors. Another special tile allows trains to be painted of a given color.
The goal is to choose the an appropriate placement of the rail pieces (straight rails, intersection, switches, …) on (a subset of) the empty tiles, so that each train reaches to a suitable destination station (i.e., each destination station receives exactly amount of trains it can hold, with the appropriate colors).
Trains that reach an empty tile, blocked tile, a destination station that cannot hold any more trains of that color, a rail piece that is not properly aligned, or try to traverse a special tile in the wrong direction result in an immediate loss.
See, e.g., [1] for a more precise description of the game.
Computational Complexity
The problem of deciding whether a Trainyard instance admits a solution (i.e., whether there is a placement of the rail pieces that correctly routes all the trains) is NP-hard [1] and in PSPACE [2].
The Trainyard Verification problem asks to decide whether a given placement of the rail pieces is a valid solution to a Trainyard instance and is PSPACE-complete [2]. An simulation of the PSPACE-completeness reduction can be found here.
Notes
An implementation of the NP-hardness reduction of [1] can be found here.
An simulation of the PSPACE-completeness reduction of [2] can be found here.
References
[1] M. Almanza, S. Leucci, A. Panconesi, “Trainyard is NP-Hard”, Theoretical Computer Science, 2018.
[2] M. Almanza, S. Leucci, A. Panconesi, “Tracks from hell - when finding a proof may be easier than checking it”, in FUN 2018.
@misc{cog:trainyard,
author = "{CoG contributors}",
title = "{Trainyard --- Complexity of Games}",
year = "2024",
url = "https://www.isnphard.com/i/trainyard/",
note = "[Online; accessed 2024-05-28]"
}
