Spiral Galaxies

A puzzle in which the player tiles a grid with polyominos with 180° rotational symmetry about given centers.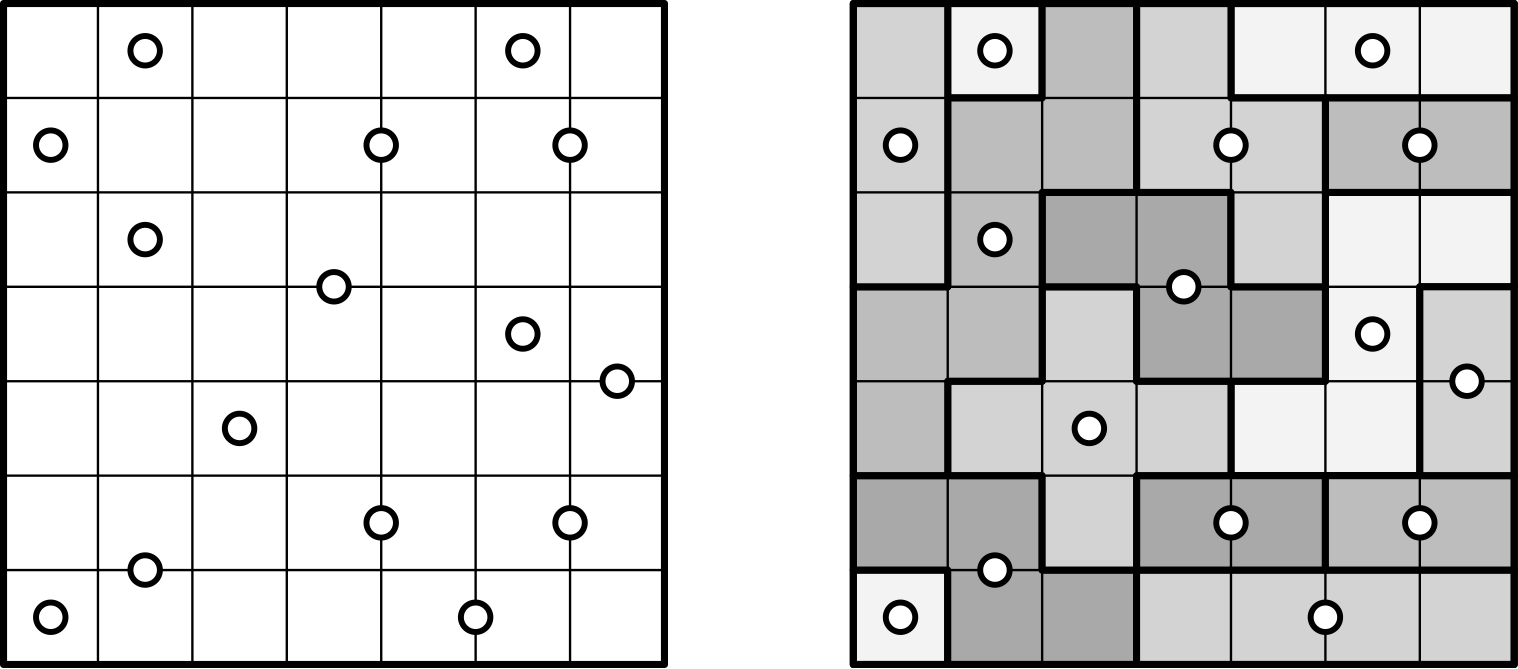

Description

Spiral Galaxies is a puzzle played on a $n \times m$ grid of squares containing a collection $C$ of center points (represented as dots). Center points can appear both in the center of a grid square, or in the center of an edge connecting two neighboring squares. The goal is to find a tiling of the grid with polyominos such that each polyomino (also called a galaxy) contains exactly one center $c \in C$ and is 180° rotationally symmetric about $c$.

The figure shows an instance of Spiral Galaxies (left) and a possible solution (right) in which the galaxies have been highlighted.

Computational complexity

The problem of deciding whether an instance of Spiral Galaxies admits a solution is NP-Complete [1].

A solution can be found in $\frac{4^{nm}}{2^{n+m}} \, \textrm{poly}(nm)$ time [2] and by an FPT algorithm parameterized in the number of corners of a solution (a corner is an internal vertex of the grid such that $1$, $3$, or $4$ of the $4$ neighboring squares belong to the same galaxy) [2].

A solution for the variant in which all galaxies need to be rectangular can be found in $|C|! \, \textrm{poly}(|C| \log nm)$ time [2].

Notes

There exist instances of Spiral Galaxies with $|C| = O(1)$ and an arbitrarily large number of corners [2].

[3] shows 36 Spiral Galaxies instances whose unique solutions form the 10 Arabic numerals and the 26 uppercase letters of the ISO basic Latin alphabet. A corresponding interactive tool is available here.

References

[1] The referenced material may not have undergone a rigorous peer review process (e.g., papers on open-access repositories, personal webpages, extended abstracts, ...) E. Friedman, “Spiral Galaxies Puzzles are NP-complete”.

[2] G. Fertin, S. Jamshidi, C. Komusiewicz, “Towards an Algorithmic Guide to Spiral Galaxies” in FUN 2014.

[3] W. Anderson, E. D. Demaine, M. L. Demaine, “Spiral Galaxies Font”, The Mathematics of Various Entertaining Subjects Volume 3: The Magic of Mathematics.

▸ ▾ Cite this page

@misc{cog:spiral-galaxies,
    author = "{CoG contributors}",
    title  = "{Spiral Galaxies --- Complexity of Games}",
    year   = "2024",
    url    = "https://www.isnphard.com/i/spiral-galaxies/",
    note   = "[Online; accessed 2024-05-28]"
}