Simultaneous Maze Solving

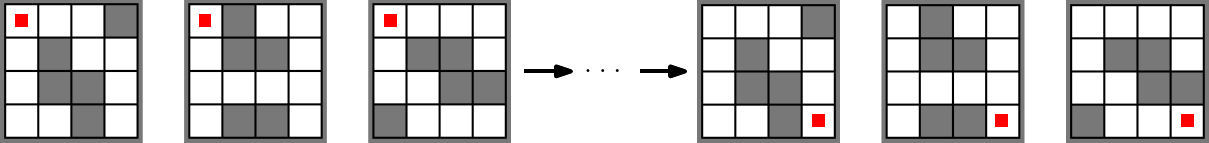
Description

Simultaneous Maze Solving is a puzzle where we are given several grid mazes and we want to find a single sequence of moves (up, down, left, right) which solves each of them.

More formally, in this problem we are given a set of mazes $\mathcal{M} \subseteq \{0,1\}^{n \times m}$, where the $0$ fields are free and the $1$ fields are blocked, and we want to know if there exists a solving sequence $s \in \{\text{up},\text{down},\text{left},\text{right}\}^k$ of length $k$. We call a sequence $s$ of moves a solving sequence if for all mazes in $\mathcal{M}$, we visit the bottom right corner when starting from the top left corner when executing $s$. A sequence $s$ is executed such that we make the moves in each maze simultaneously, and we only stay on the unblocked (i.e., zero) fields of the maze. If we walk in direction of a blocked (i.e., one) field of a maze, then the move is not executed in this maze but it still possibly executed in the others.

Computational Complexity

The problem has been shown to be NP-complete via a reduction from CNF-SAT [1].

The variant where one wants to find a sequence for all solvable mazes of a certain size $n \times m$ is in PSPACE. The length of such a sequence is lower bounded by $\Omega(nm)$ and upper bounded by $O((nm)^3)$ [1].

Notes

A playable version of the NP-hardness reduction of [1] is available here.

References

[1] Stefan Funke, André Nusser, and Sabine Storandt, “The Simultaneous Maze Solving Problem”, in AAAI 2017.

@misc{cog:simultaneous-maze-solving,
    author = "{CoG contributors}",
    title  = "{Simultaneous Maze Solving --- Complexity of Games}",
    year   = "2024",
    url    = "https://www.isnphard.com/i/simultaneous-maze-solving/",
    note   = "[Online; accessed 2024-04-13]"
}