
Shannon Switching Game (Gale, Bridg-it)
Blue and Red alternate in coloring the edges of a graph $G$. Blue wants to connect two distinguished vertices $s,t$ of $G$ with a blue path. Red wants to select a $s$-$t$ edge-cut.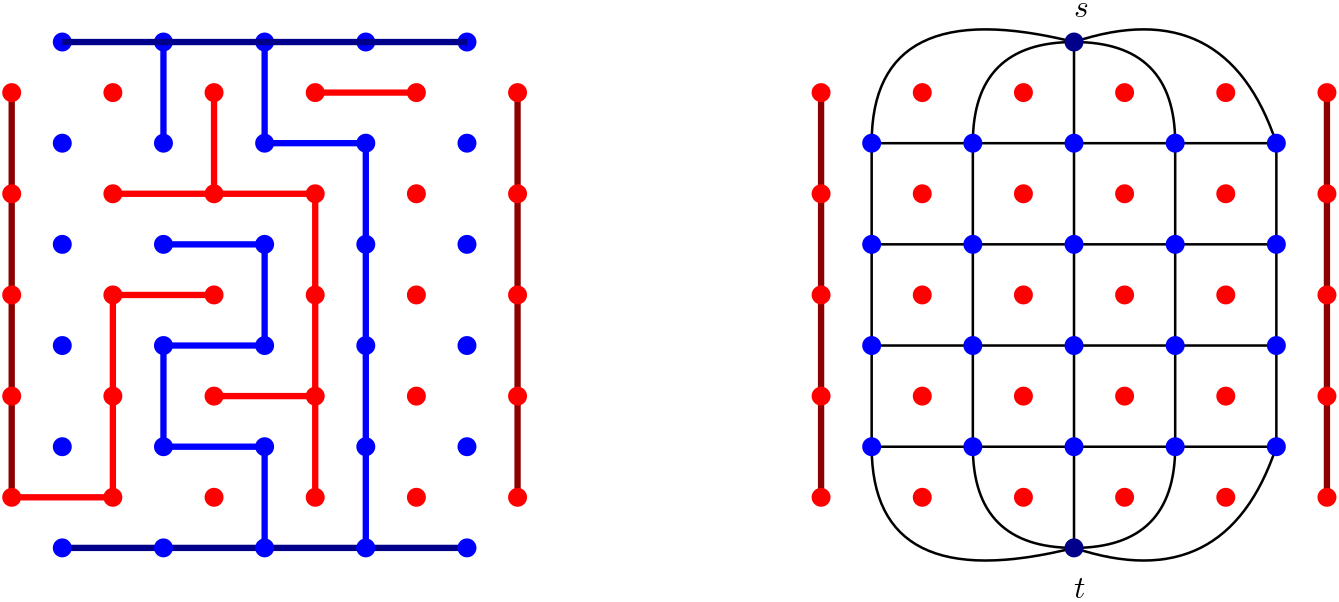
Description
Given a connected graph $G=(V,E)$ and two distinct vertices $s,t \in V$, two players blue and red take turns in coloring an uncolored edge of their respective color. Initially all the edges are uncolored. Blue wins if the set of blue edges contains a path from a $s$ to $t$. Red wins if every path from $s$ to $t$ contains at least one red edge, i.e., if the red edges form a $s$-$t$ edge-cut.
A special version of the game is called Gale or Bridg-it. This game starts with two partially overlapping $n \times (n-1)$ and $(n-1) \times n$ grids of dots, one blue and one red, respectively (see the left picture). Red and Blue take turns in drawing an horizontal or vertical segment between two neighboring dots of their color. The drawn segment must not cross any other segment. The blue (resp. red) player wins by connecting a blue (resp. red) dot on the top (resp. left) side to a blue (resp. red) dot on the bottom (resp. right) side with a blue (resp. red) path. Sometimes the blue dots on the top and bottom sides (resp. the red dots on left and right sides) are already connected by two blue (resp. red) paths in the initial configuration, as any strategy playing any such move is suboptimal.
Gale is equivalent to the Shannon switching game in which the graph $G$ consists of a $n \times (n-1)$ grid (including edges and vertices) in which the vertices on the top side have been identified into a new vertex $s$ and those on the bottom side have been identified into a new vertex $t$. Coloring an edge of $G$ with blue is equivalent to drawing the corresponding blue segment. Coloring an edge of $G$ with red is equivalent to drawing the unique red segment that intersects the blue segment corresponding to the colored edge (see the right picture).
Computational complexity
The problem of deciding whether blue has a winning strategy for a given instance of the Shannon Switching Game is in P. [1]
The problem of computing a winning strategy for the winning player is also in P. [1] [2]
In Bridg-It the first player to move can always for a win, as can be seen by a strategy stealing argument. Oliver Gross provided a simple explicit strategy [3].
Notes
The version of the game in which vertices are colored instead of edges is known as Shannon Switching Game on Vertices and is a generalization of Hex.
References
[1] A. Lehman, “A Solution to the Shannon Switching Game”, Journal of the Society for Industrial and Applied Mathematics, 1964.
[2] J. Bruno, L. Weinberg, “A Constructive Graph-Theoretic Solution of the Shannon Switching Game”, IEEE Transactions on Circuit Theory, 1970.
[3] M. Gardner, “New Mathematical Diversions”, 1995.
@misc{cog:shannon-switching-game,
author = "{CoG contributors}",
title = "{Shannon Switching Game (Gale, Bridg-it) --- Complexity of Games}",
year = "2024",
url = "https://www.isnphard.com/i/shannon-switching-game/",
note = "[Online; accessed 2024-05-28]"
}
