
Shannon Switching Game on Vertices (Hex)
Blue and Red alternate in coloring the vertices of a graph $G$. Blue wants to connect two distinguished vertices $s,t$ of $G$ with a blue path. Red wants to select a $s$-$t$ vertex-cut.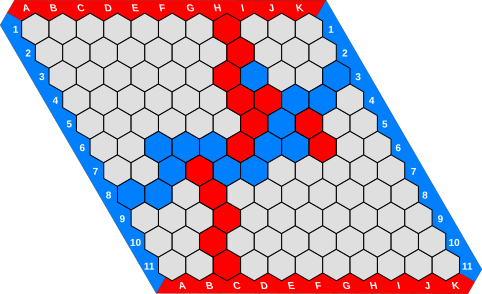
Description
Given a connected graph $G=(V,E)$ and two distinct vertices $s,t \in V$, two players blue and red take turns in coloring an uncolored vertex in $V \setminus \{ s, t \}$ of their respective color. Initially all the vertices are uncolored. Blue wins if the set of blue vertices contains a path from a neighbor of $s$ to a neighbor of $t$. Red wins if every path from $s$ to $t$ contains at least one red vertex, i.e., if the red vertices form a $s$-$t$ vertex-cut.
Hex is a popular special case of this game that is played by coloring the hexagons of a rhombus-shaped hexagonal grid. Two opposing sides of the grid are blue, while the remaining two sides are red. Blue (resp. red) wins by connecting the two blue (resp. red) sides with a blue (resp. red), where two hexagons are considered adjacent if they share an edge.
An instance of Hex can be thought as an instance of the Shannon switching game on vertices in which the vertices in $V \setminus \{s, t\}$ are the hexagons in the grid, and $s$ and $t$ are adjacent to all the hexagons on the two opposing blue sides, respectively.
The classical version of Hex, shown in the picture, is played on a $11 \times 11$ grid.
Computational complexity
The game cannot end in a draw: if all the vertices are colored and there is no blue path from $s$ to $t$, then there is a red $s$-$t$ vertex cut.
In a final configuration of Hex there is either blue or a red path connecting the sides of the grid having the corresponding color [1]. A strategy stealing argument shows that, in Hex, the first player to move has a winning strategy. [2]
In the Misère version of Hex (the first player to connect their two sides with a path of their color loses) the first player has a winning strategy on $n \times n$ rhombus shaped grids when $n$ is even, and the second player has a winning strategy when $n$ is odd. [4]
It is PSPACE-complete to decide whether a player has a winning strategy in the Shannon switching game on vertices [3], even on planar graphs [5].
Notes
The version of the game in which edges are colored instead of vertices is known as Shannon Switching Game.
References
[1] David Gale, “The Game of Hex and Brouwer Fixed-Point Theorem”, The American Mathematical Monthly, 1979.
[2] Martin Gardner, “Hexaflexagons and Other Mathematical Diversions: The First Scientific American Book of Puzzles and Games”, 1988.
[3] S. Even, R. E. Tarjan, “A combinatorial problem which is complete in polynomial space”, in STOC 1975.
[4] R. B.Haywarda, B. Toft, P. Henderson, “How to play Reverse Hex”, Discrete Mathematics, 2012.
[5] S. Reisch, “Hex ist PSPACE-vollständig”, Acta Informatica, 1981.
@misc{cog:shannon-switching-game-on-vertices,
author = "{CoG contributors}",
title = "{Shannon Switching Game on Vertices (Hex) --- Complexity of Games}",
year = "2024",
url = "https://www.isnphard.com/i/shannon-switching-game-on-vertices/",
note = "[Online; accessed 2024-05-28]"
}
