Peg Solitaire is NP-Hard
What is this?
This page deals with a generalized version of Peg Solitaire (also known as Hi-Q) where the board is allowed to a square of arbitrary size.
The problem of deciding whether an instance of generalized Peg Solitaire is winnable has been proven to be NP-complete in Ryuhei Uehara and Shigeki Iwata: Generalized Hi-Q is NP-complete (1990), via a polynomial-time reduction from the Hamiltonian Cycle problem in a planar graph where indegrees and outdegrees are upper-bounded by two.
This page hosts a playable implementation of this reduction for the following graph:
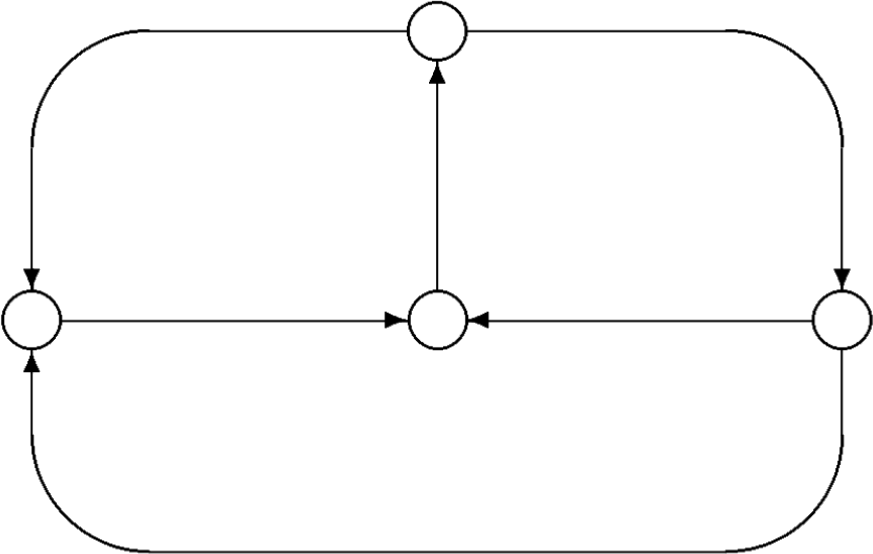
To make a move, just click on a peg in the playing board, then click on a valid destination.
| Playing board |
|---|
| Winning state |
|---|
| Solution (click to see the next step) |
|---|

