Bejeweled, Candy Crush and other match-three games are (NP-)Hard!
What is this all about?

This is an implementation of the reduction provided in the paper Bejeweled, Candy Crush and other Match-Three Games are (NP)-Hard which has been accepted for presentation at the 2014 IEEE Conference on Computational Intelligence and Games (CIG 2014). To find more about what NP-Hard means you can read this blog post or the corresponding page on Wikipedia.
About the authors
We are an Italian group of three people: Luciano Gualà, Stefano Leucci, and Emanuele Natale. We had the weird idea to spend our weekends proving that Candy Crush Saga is NP-Hard. We also thought that it was nice to put online an implementation of our hardness reduction... so here it is!Rules
Swap two adjacent gems in order to match three or more gems of the same kind. The matched gems will pop, and the gems above will fall. It is possible to have chains of pops.
For a complete understanding of what's going on please read the paper on ArXiv.
In a nutshell (for those "tl;dr" folks): you can swap one or two gems on each choice wire from the top one to the bottom one, then you have to traverse the goal wire to reach the goal gem. Popping a wire means setting the corresponing variable to true.
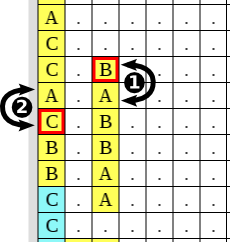
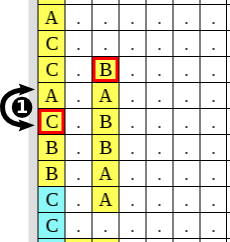
Start at the choice wire for the first variable. You will be able to pop the goal gem if and only if the formula is satisfable.
Try for yourself
Enter a 1-in-3 positive SAT formula*:
.
*Actually, we also support formulae with less than three variables per clause (but not more).
Can you pop the goal gem?

